 Domino fractions est une application (gratuite et sans publicité) créée par Christophe Auclair, enseignant en collège.
Domino fractions est une application (gratuite et sans publicité) créée par Christophe Auclair, enseignant en collège.
Elle permet de… jouer en calculant des fractions.
Au lancement, un menu (unique) apparaît.

Vous pouvez alors :
- fixer le nombre de dominos avec lequel vous allez jouer;
- choisir de manipuler des fractions ou des écritures fractionnaires (avec ou sans nombre à virgule, enfin!);
- sélectionner une ou plusieurs opérations possibles parmi l’addition, la soustraction et la division de fraction.
Nous sélectionnons 10 dominos, sans nombre relatifs, avec des divisions uniquement et nous démarrons ainsi une partie.
Au premier coup, nous choisissons (un peu au hasard) et plaçons un premier domino.
Afin de placer un second domino, réfléchissons à partir de l’écran obtenu.
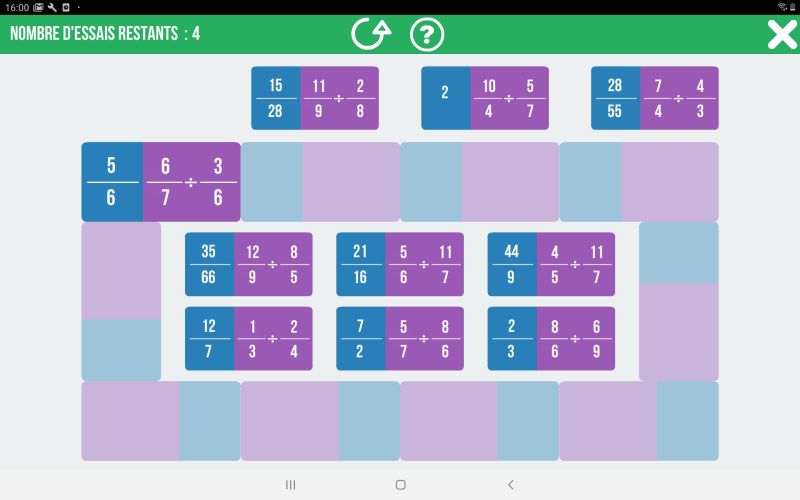
Le premier domino peut être compléter :
- par la droite avec un domino proposant dans sa partie gauche une fraction égale à \(\frac{6}{7} \div \frac{3}{6} \).
- par le bas, avec un domino dont l’expression (à droite) est égale après calcul à \(\frac{5}{6}\).
Un peu de calcul mental nous permet de placer à droite le domino suivant :

En effet après calcul et simplification :
\( \frac{6}{7} \div \frac{3}{6} = \frac{6}{7} \times \frac{6}{3} = \frac{ 6 \times 6}{7 \times 3} = \frac{ 6 \times 2 \times 3}{7 \times 3} =\frac{12}{7}\).
Pour déterminer quel domino nous pouvons placer « en bas », cherchons quel domino propose un calcul égal à \(\frac{5}{6}\).
Ce sera celui-ci :

En effet : \( \frac{12}{9} \div \frac{8}{5} = \frac{12}{9} \times \frac{5}{8} = \frac{12 \times 5}{9 \times 8} \frac{4 \times 4 \times 5}{9 \times 4 \times 2} = \frac{5}{6} \).
Plaçons ces deux dominos, ce qui amène cette nouvelle « position » :
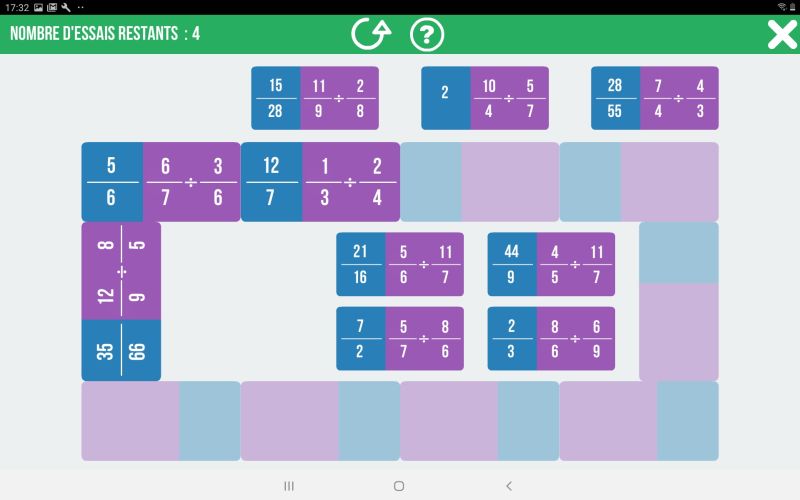
Et le jeu continue.
L’application est disponible pour Android, IOS et Windows, en téléchargement sur le site de l’académie de Dijon à cette adresse : http://mathematiques.ac-dijon.fr/spip.php?article200.
