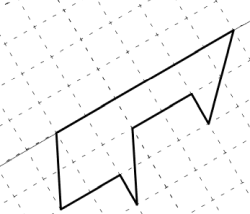Sur le site de l’APMEP, deux fiches d’exercices de Michel Suquet  proposant des tracés de figures, plus précisément quatre polygones :

• la première fiche permet de tracer le symétrique de chaque figure à l’aide d’un quadrillage;
• la seconde fiche présente les mêmes figures sur une page blanche, et il faudra donc utiliser les instruments de géométrie.

En vidéo sur la chaîne YouTube.

Avec Geogebra nous traçons un polygone à trois côtés… un triangle donc.  Afin de tracer la médiatrice de chaque côté du triangle, nous testons successivement deux approches :

1. L’outil « Cercle (centre-rayon) » va nous permettre de placer deux points équidistants de chaque extrémité d’un côté triangle, puis de le relier, tracer ainsi la médiatrice de ce côté.
2. L’outil « Milieu ou centre » associé à l’outil « droite perpendiculaire » offrira un moyen plus simple de tracer une médiatrice.

Enfin, lorsque nous aurons tracé les trois médiatrices, nous déformerons le triangle en déplaçant les sommets afin de conjecturer une propriété.

lire plus…

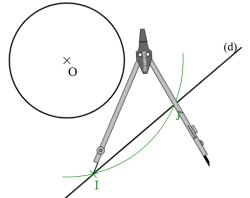Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire le symétrique d’un cercle par une droite (d).

On considère un cercle de centre O et de rayon r.

• Placer le point O’, symétrique du point O par la droite (d).
• Tracer le cercle de centre O et de rayon r.

C’esi ici.

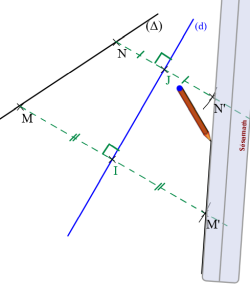Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire le symétrique d’un segment [MN] par une droite (d) avec une équerre et un compas.

• Placer le point M’, symétrique du point M par la droite (d).
• Placer le point N’, symétrique du point N par la droite (d).
• Tracer la droite (M’N’).

C’esi ici.

lire plus…

Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire le symétrique d’un segment [AB] par une droite (d) avec une équerre et un compas.

• Placer le point A’, symétrique du point A par la droite (d).
• Placer le point B’, symétrique du point B par la droite (d).
• Tracer le segment [A’B’].

C’esi ici.

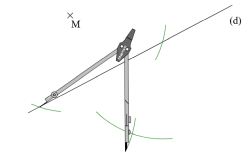Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire le symétrique d’un point M par une droite (d) avec un compas.

• Tracer deux arcs de cercle de centre M coupant la droite (d).
• En prenant comme centre chacun de ces deux points et en gardant le même écartement du compas (même rayon) tracer des arcs de cercle.
• Coder la figure.
• Nommer M‘ l’intersection de ces deux arcs de cercle.
• Le point M‘ est le symétrique du point M par rapport à la droite (d).

C’est ici.

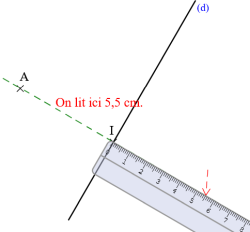Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire le symétrique d’un point A par une droite (d).

• Placer l’équerre sur le point A et le long de la droite (d).
• Placer la règle le long de l’équerre, perpendiculairement à la droite (d).
• Tracer la droite passant par A et perpendiculaire à (d).
• Appeler I le point d’intersection des deux cercles.
• Placer A‘ sur la droite tracée en reportant la longueur AI.
• Coder la figure.

C’est ici.

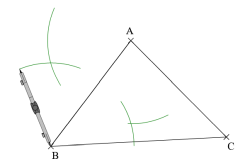Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire la médiatrice d’un coté d’un triangle  avec un compas.

• Tracer un triangle [ABC].
• Tracer un arc de cercle de centre A et de rayon supérieur à la moitié de la longueur [AB].
• Tracer un arc de cercle de centre B et de rayon identique.
• Tracer la droite passant par les intersections de ces deux arcs de cercle.
• Coder la figure.

C’est ici.

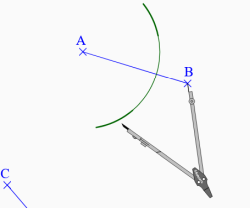Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire la médiatrice d’un segment avec un compas.

• Tracer un segment [AB].
• Tracer un cercle de centre A et de rayon supérieur à la moitié de la longueur [AB].
• Tracer un cercle de centre B et de rayon identique.
• Tracer la droite passant par les intersections de ces deux cercles.
• Coder la figure.

C’est ici. lire plus…

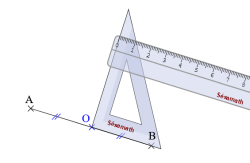Cette animation de la bibliothèque Instrumenpoche de l’association Sesamath montre comment construire la médiatrice d’un segment avec une équerre.

• Placer le point O d’un segment [AB].
• Avec l’équerre et la règle, construire la droite perpendiculaire à [AB] passant par O.
• Coder la figure.

C’est ici.

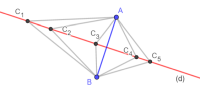Je vous propose une activité d’introduction de la médiatrice d’un segment de droite, avec correction :

• tracer une figure en exécutant un programme de construction;
• proposer une définition de la médiatrice d’un segment;
• proposer une propriété de la médiatrice.

Vous pouvez télécharger le document ici.

lire plus…